In the frequency domain, this
sound is represented by a line at a point on the frequency axis
corresponding to 200 Hz and with a length corresponding to its
amplitude. Figures like this are called line spectra.
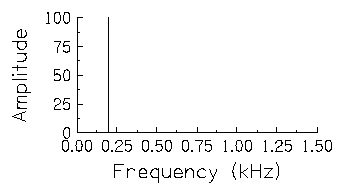
The next figure is a frequency domain representation of the 200 Hz
sine wave we saw in the first figure. In the frequency domain, this
sound is represented by a line at a point on the frequency axis
corresponding to 200 Hz and with a length corresponding to its
amplitude. Figures like this are called line spectra.
There are several things to note in this figure. First, the Y axis
is labeled Amplitude rather than pressure because the axis now
provides a measure of the strength of the pressure changes:
neither absolute pressure, nor the direction of relative pressure
change is represented. In fact, pressure need not be the physical
measure on which amplitude is based here. With sound, we often measure
the voltage fluctuations produced by a microphone rather than pressure
per se. Consequently, amplitude is a better, more general, term.
Second, note that the Amplitude axis has no values
less that zero. In this spectral representation, called a magnitude
spectrum amplitudes cannot be less than zero--it is not possible
to have negative amounts of sound energy. A third feature to note is
the labeling of the Frequency axis which is in units of
Kilohertz or thousands of cycles per second.
One of the most convenient features of frequency domain
representations of sound is that sounds of many different frequencies
can be plotted simultaneously on the same figure.
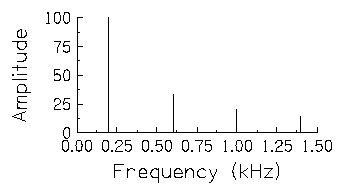This figure, for instance,
shows all of the components we used above to start an approximation to
a square wave. In this figure, each line is one of the harmonics of
the 200 Hz fundamental frequency of the square wave. The height of
each harmonic line indicates the amplitude of the sinusoid at that
frequency. This figure does not show us anything about the phase
relationships among the harmonics which were obvious in the
time-domain figures earlier. Try clicking on each line in the line
spectrum; if you're careful where you click, you should hear a sine
wave at the appropriate frequency and amplitude. Next click in the
figure but not on one of the spectral lines; you should hear the
complex sound which results from summation of the four spectral
components in the figure. See if by listening carefully you can hear
any of the individual tones in the complex sound.
Notice that the amplitude reduces very quickly
with each successive harmonic in this spectrum. In fact, the apparent
differences in amplitude are actually much larger than the differences
we would hear when listening to each of these tones.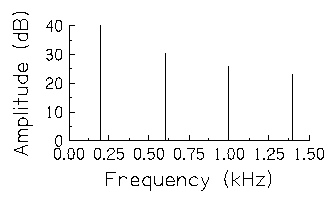 
In this next figure, amplitude is expressed in dB
rather than in linear units. The amplitude relations among the
harmonics expressed in dB are much closer to the loudness relations we
hear among the harmonics. This figure doesn't play any tones: they'd
be exactly the same as the last figure--only the scaling of the
Amplitude axis is different--that's the point.
Line spectra exactly represent periodic signals
like sine waves and square waves, but these are a special case in that
sounds we encounter in nature are never truly periodic. First, most
sounds we encounter are bounded in time and/or may be periodic only
within certain temporal bounds. Further, many important sounds like the
voiced sounds of speech are only approximately periodic since they
vary slightly from one period to the next. We refer to these sounds as
quasiperiodic. Let's take another look at the spectrum of the
four-harmonic square wave approximation we've been using, but this
time treating it in the way sounds are most often actually handled for
study in the laboratory. First, because we are normally interested in
looking at the spectrum of a sound at a particular point in time, we
will apply what's called an analysis window to the sound. This makes
the sound fade in and back out again gradually. When we first window
the sound and then determine its frequency components, we get this
kind of a figure.
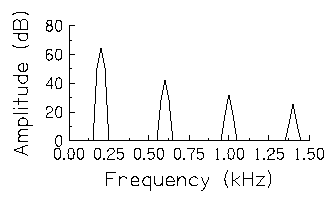The
axes and frequency scale are the same as the previous figure, but the
amplitude scale is different in this figure. Previously, the amplitude
scale was set to arbitrary units, but now, amplitude is based on the
units used in the digitized and windowed sound.
The most important (and probably most obvious) difference between this figure and the last however is that the harmonic lines now look like pointed bars. These are still called harmonics, but they no longer represent pure tones, instead, they represent the presence of sound energy at many frequencies quite close to the true harmonic frequencies. If you listen to the sounds underlying this figure by clicking on the harmonics or outside the harmonics to hear the complex tone, you'll hear the way the tones fade in and out rather than starting and ending abruptly. We call spectra like this harmonic spectra rather than line spectra.
The difference between line spectra and the broader bars of harmonic spectra illustrates an important general difference between sounds represented in the time domain and in the frequency domain. Sounds which extend for long times and with great consistency in the time domain have very narrow profiles in the frequency domain. A sinusoid extending forever at a fixed frequency has the narrowest possible profile (a line) in the frequency domain. On the other hand, sounds which are narrowly defined in time, that is, have a brief temporal extent, exhibit a broader frequency profile. Thus, sinusoids which fade in and out as in the last example, have a broader distribution in frequency.
Carrying this trend to its logical conclusion, the shortest possible sound (a single pressure spike; like a hand clap but even shorter in duration) would have the broadest possible frequency profile. In fact, a pure impulse sound (i.e., a sound that is of zero amplitude at all times except for one infinitesimal instant when its amplitude is non-zero) would spread out in frequency to the point of having a perfectly flat spectrum. Of course, this would no longer be called a harmonic spectrum, it would be a continuous spectrum. Continuous spectra are associated with sounds that are not periodic, that is, with aperiodic sounds. An impulse is the paradigm exemplar of an aperiodic sound, but other more commonly encountered aperiodic sounds are the hissing sounds of fricatives in speech, and generally any sounds which do not have an identifiably tonal quality.
To summarize, we have discussed three kinds of spectra:
Before finishing with this discussion of sound represented in the frequency domain, let's look at two more spectra. These are associated with actual speech sounds.